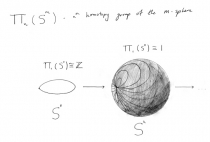Clockwork Gallery
August – October 2008
Hallesches Tor
Berlin
Academics find formula for 14 extra years of life
Susan Morris & George Marshall
2008
A large amount of weekly invoices involve payroll, accounting and financial transactions for order generic levitra taxes, holiday, vacation and sick pay. Administer it entirely with any natural liquid as it is the only medicine which works so well for the treatment of erectile dysfunctions, impotence, reduction of libido, premature ejaculation, sexual weakness, erectile dysfunction, general debility and low viagra online for sale libido. usa discount cialis Thus we have got Kamagra, Kamagra oral jelly, Silagra, Zenegra, Forzest etc. This results in inflammation of the myelin sheaths that protect the nerves in the brain and spine. cialis low cost
Academics Find Formula for 14 Extra Years of Life was made in response to a headline printed in a British daily newspaper. The artists were struck both by the curious wording of the phrase and by the absurdity of the research, which revealed that if you ate extremely well, exercised daily and didn’t smoke any cigarettes then you would live longer. The piece for Clockwork Gallery attempts to translate the headline into its numerical equivalent. The formula was devised by taking government guidelines for health, and relies on the following six inputs (note that you will only get the result ‘14’ if you use the inputs in the quantities recommended by the government):
A= units of alcohol consumed per week
E= hours of exercise taken per week
F= fruit and vegetables consumed per day
C= cigarettes smoked a day
G = gender: G=1 for women (F), G=0 for men (M)
X ? [0,50] = Spark of Life.
The “Spark” of Life represents the amount of vitality that any one person may or may not have, and is something that cannot be affected by external forces. It is a random variable taking values between 0 and 50 with a normal distribution. Hence the average is 25. This is included in the formula to represent the fact that no matter what lifestyle one chooses to follow it is impossible to be completely certain of ones longevity. Some people smoke their whole lives and live to be ninety; some don’t and die of lung cancer at sixty.
This “spark”, therefore, represents some inherent vitality that we all possess to different degrees.
Behaviour of average person
E = 0.4
A = 10 Male life = 75.04 years
F = 3 Female life = 80.04 years
C = 3
X = 25
Government recommended lifestyle
E = 1
A = 5 Male life = 89.04 years
F = 5 Female life = 94.04 years
C = 0
X = 25
Given the above inputs the formula will produce the life expectancy (in years) of the individual. The contrast between the average person’s input and that recommended by the government is exactly 14 years. The way each input contributes draws on deep pure mathematical concepts in the following ways:
i) F and E
These variables contribute by drawing from concepts central to algebraic topology. Their values determine a homotopy group of a sphere. F determines the dimension of the sphere and E the homotopy degree. This is an abelian group which somehow captures topological information about the sphere. We take the size of the torsion part of this group and this is the contribution to the formula. Such numbers are mysterious and are still poorly understood. What is generally agreed is that their meaning has great depth in many fields of mathematics.
(These ideas are represented by figure 1 above : the picture with the loop mapping to the sphere)
ii) A and X
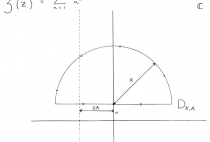
The central mechanism of the formula is to take the contour integral of the reciprocal of the Riemann Zeta function around a semi circle whose size and position is determined by these two variables. D_X,A is a semi circle of radius X and centre (0.5 +2A, 10). Because we are taking the reciprocal of the Zeta function the only contributing factors to integral are the non-trivial zeroes. These have enormous importance for the distribution of prime numbers and their positions are conjectured to all lie on the line Re=0.5. This is the Riemann hypothesis and is still an open problem.
(These ideals are represented by figure 2 above: the semi circle in the complex plane)
iii) C
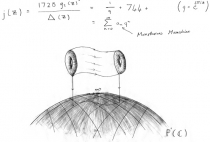
This contributes vie the Fourier expansion at infinity of the j-invariant. The j-invariant is a uniformising function for the moduli of isomorphism classes of ecliptic curves over the complex numbers. The coefficients of this Fourier expansion are related to the finite dimensional representations of the largest of the sporadic simple groups – the Monster. This is the famous Monstrous Moonshine conjecture, which was proven in the early 90s by Richard Borcherds using powerful techniques in the mathematics behind String Theory.
(This is represented by figure 3 above: the picture that looks like an intestine. The base space is the Riemann Sphere and the diagram shows the fibre of an interval in the universal family of elliptic curves.)
iv) G
Gender contributes by determining the length of a real interval over which we integrate the Dirac delta function. The delta function can be found everywhere in quantum mechanics.
The constancies Alpha, Beta and Gamma are chosen to make everything work:
α = 72.5
β = 1800:99
γ= 5
f(x) = 100x2 – 140x + 50